PoW 比你想象的更安全
PoW 的安全性风险在于区块 revert/reorg,从而导致双花。只要有一个诚实矿工,用户的状态/资产就不会计算错误,只有可能出现因区块重整导致的双花交易损失。因此 PoW 的核心安全假设就是 N 个区块后交易就几乎不会被 revert 了,例如 Bitcoin 普遍认为 6 区块甚至更少即可。
显然,6确认的 BTC 肯定比1确认更安全,那么 PoW 确认数和安全性是线性关系吗?并不是,推翻区块的难度随着区块深度指数增长,这个指数增长具体的参数已经有几十篇论文在讨论了。随着时间的推移,大家发现“NC比从前以为的更安全”。
根据 Ren Zhang 博士的计算,假设敌手算力占比30%,要实现比特币中孤块率为0、6个块确认的安全性,当 CKB 的孤块率设定成 2.5% 的时候,需要23.29个块确认即可达到相同的安全性 。通过这样的等价关系,我们可以在后续的讨论中方便地讨论 RGB++ 协议中各种典型操作的安全性。
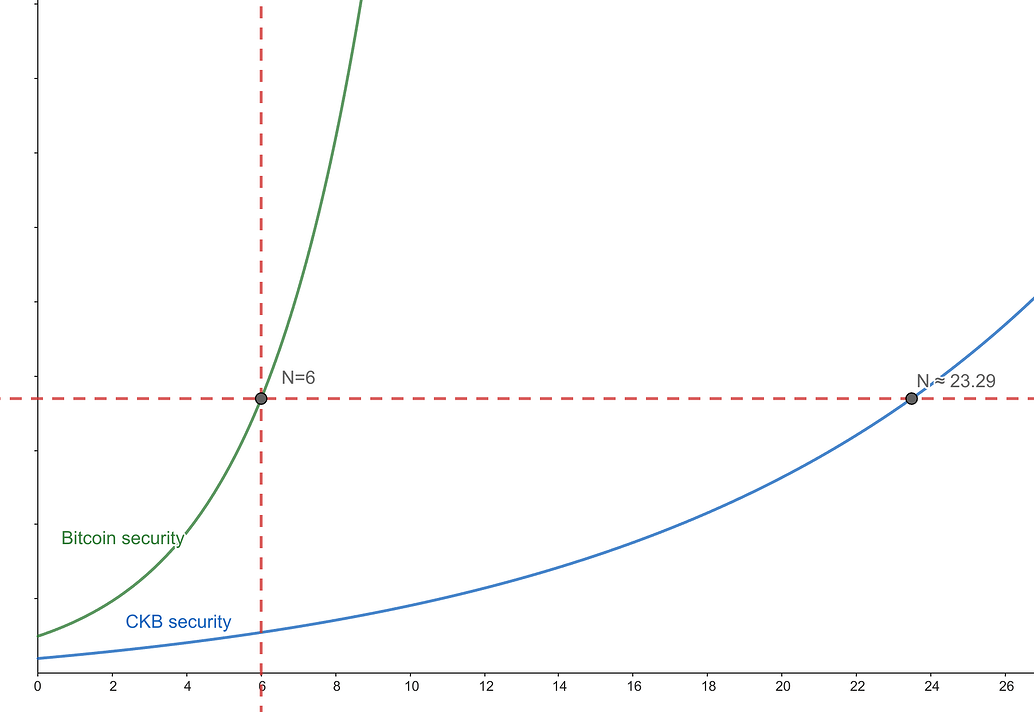
PoW 安全性的示意图(非理论计算)
RGB 的安全性
RGB 通过一次性密封和客户端验证的方式实现了在 Bitcoin UTXO 上绑定 RGB 的状态和合约,为 Bitcoin 提供了图灵完备的扩展。交易安全性有两类,一类是状态计算的正确性;一类是交易确定性,即双花风险。客户端验证确保了状态计算的正确性,每个人负责自己的状态,不依赖任何第三方。而基于 BTC UTXO 的一次性密封确保了双花 RGB 的难度和双花 BTC 的难度相同。因此,我们可以说 RGB 100% 继承了 Bitcoin 的安全性。用户需要多安全,就按照比例等待多少个 BTC 确认即可。
RGB++ �的安全性
L1 交易安全性
RGB++ 的 L1 交易指的是 RGB++ 交易的 UTXO 的"持有人" 是 Bitcoin 的 UTXO。即只有消费 Bitcoin UTXO 才能操作或更新 RGB++ UTXO。这种情况下,虽然每一笔 RGB++ 交易都同步发起一笔 CKB 交易,但其安全性和 CKB 没有关系,CKB 仅作为 DA 和状态公示来使用。这种情况下,RGB++ L1 的交易安全性和 RGB 交易相同,也是完全继承了 BTC 的安全性。
L2 交易安全性
L2 交易即 100% 发生在 CKB 上的交易,显然它的安全性 100% 由 CKB 负责。但由于开篇提出的 PoW 安全的非线性特性,24个区块的 ckb 确认即可等价于 6 确认的 BTC 确认,因此我们也可以说 L2 交易安全性与 L1 交易安全性等价(需要更多区块确认,但事实上更短确认时间)。
能做到这一点的前提是 RGB++ 的同构映射链必须是 PoW 的,如果它是 PoS 的链,无论等待多少个区块,它安全性上限都是 PoS 的 stake 量,无法与 Bitcoin 安全性等价。
Jump 操作
RGB++ 协议中用户的资产既可以在 Bitcoin 上流转,也可以随时到 CKB 上流转,或者反向操作。在切换的过程不需要跨链桥,更不需要信任任何多签方。我们将资产或状态在 Bitcoin 上和 CKB 上流转的切换称为 Jump。Jump 操作前后,影响 RBG++ 协议安全性的核心点在于:
- 一次性密封条,从使用 Bitcoin UTXO 变为使用 CKB UTXO,或相反
- 客户端验证所需要的数据保持不变,都是 CKB 上的同构绑定交易
Jump 操作时,用户需要在两条链上分别等待足够的区块数,以获得安全性。
兼顾用户体验
根据上面的讨论,等待足够多的区块数确实可以获得足够的安全性,但用户体验实在太差了。考虑平庸的方案,每个 RGB++ L1 交易要等待 6 个 BTC 确认再进行下一次操作,每个 L2 交易要等待 24 个 CKB 确认再进行下一次操作,而 Jump 操作则需要等待 6 BTC + 24 CKB 确认。能否对这个方案进行优化呢?
RGB 收款方 UTXO 的优化
考虑原 RGB 协议,为了实现交易隐私性,Bitcoin 上发起的 RGB 交易的收款方(以一个 Bitcoin utxo 表达)和这笔 Bitcoin 交易的 output 并不一致。这使得观察者无法通过追踪 bitcoin 交易的方式来追踪 RGB 交易。
但在 RGB++ 协议中,所有的 RGB++ 层交易都同构绑定并公示在 CKB 上,尽管极大地简化了用户的交易验证难度,也较为遗憾地损失了 RGB 协议的隐匿性(RGB++ 协议可以利用 CKB 的隐私层引入更为强大的隐私属性 )。所以 RGB++ 协议在收款人方面做了调整,它不要求收款方预先提供一个自己的 UTXO,而只需要提供一个收款地址,RGB++ 交易本身在构造 BTC 交易时会生成一个 UTXO 指向该收款人地址。这样就可以完成非交互式转账,大幅简化了用户的操作流程。注意下面的示意图做了一些简化,为了实现同构绑定,某些包含在 BTC TX 和 CKB TX 中的字段不会被包含在 commitment 中,以防止出现互相包含的矛盾。
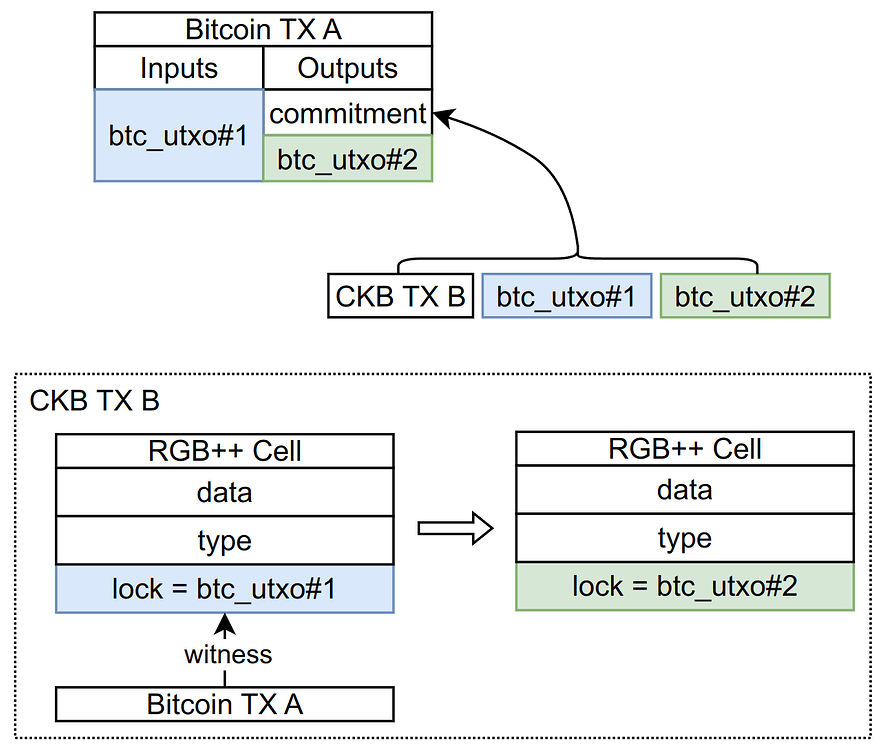
交易串接
上面的 RGB 非交互式转账的优化不仅仅有利于提升用户体验,对于交易确认的优化也有本质的作用。
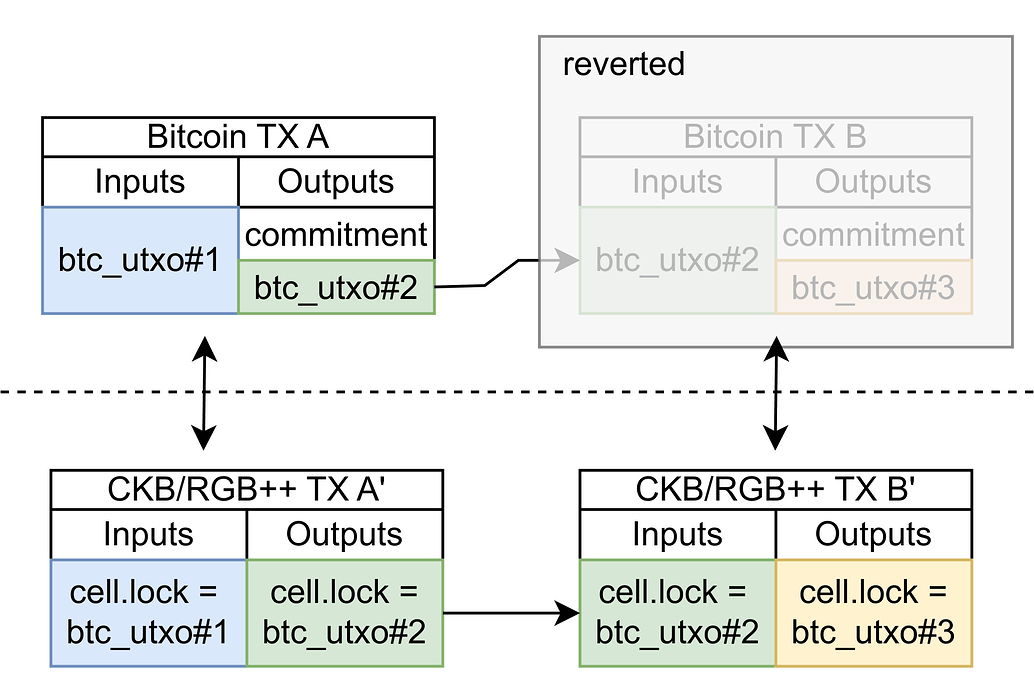
首先对于一个诚实的用户,尽管区块 reorg 经常发生,但只要该用户不主动进行双花交易,BTC 链上打包的用户交易是不变的,因此不会影响到 CKB 链上的 RGB++ 资产和状态。
考虑一笔 L1 RGB++ 交易,假设为了用户体验我们允许单块 BTC 交易确认即可发起同构交易,即在 CKB 构造同步的 RGB++ 资产交易。此时,对于恶意用户,TA 可能构造一笔新的 BTC 交易,取代之前的 BTC TX B,使得 CKB TX B‘ 找不到对应的 BTC 交易,但这时 CKB TX B’ 已经上链。这里的后果是,在 BTC 上被双花的 btc_utxo#2 在 CKB 上的同构映射 cell 已经在 CKB TX B’ 中消耗了,即使用户双花了 BTC 上的 utxo,他也无法双花 RGB++ 的资产,同时先前交��易生成的 RGB++ cell 输出( lock 为 btc_utxo#3)也因为链式交易的失效而被用就锁定。所以恶意用户在 BTC 上做双花交易不会有任何收益,还会导致自己的资产失效。
考虑一笔 L2 RGB++ 交易,它 100% 运行在 CKB 上,因此我们只需要符合原来的交易逻辑即可,即也可以在 dapp 中获得连续操作的体验。
最后考虑一笔 Jump 操作,用户将 RGB++ 资产从一个 Bitcoin UTXO 中转到一个 CKB 地址上,后续的操作会持续发生在 CKB 上,此时我们需要考虑因 Bitcoin TX revert 造成的 CKB 上资产复制的问题。
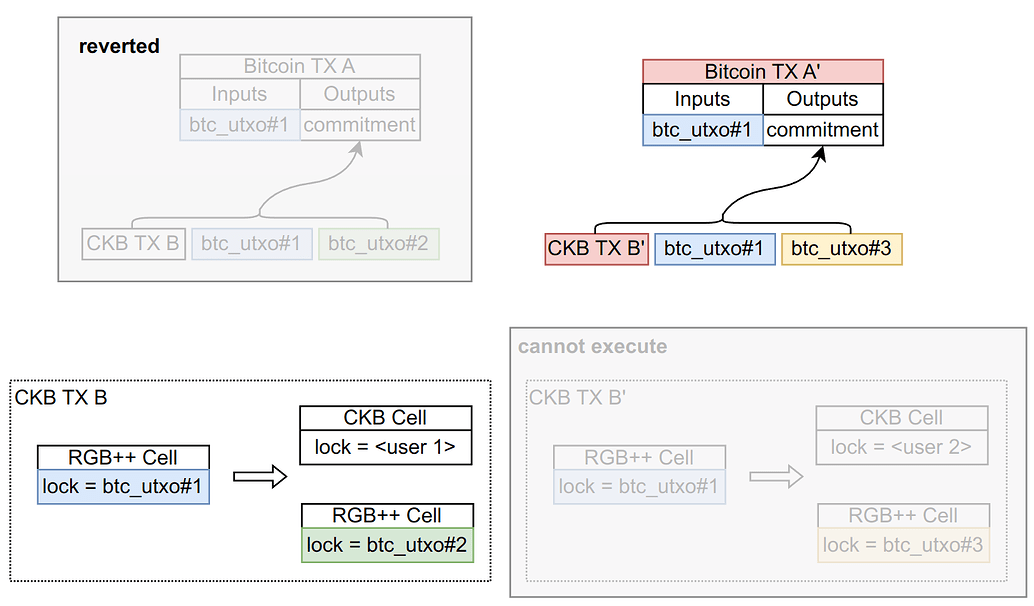
考虑上面的交易,BTC_TX_A 和 CKB_TX_B 同构绑定,之后 BTC_TX_A 被重构成 BTC_TX_A’,此时同构绑定的交易 CKB_TX_B’ 无法通过 ckb 共识上链,因为它依赖的 input (lock= btc_utxo#1)已经在 CKB_TX_B 中被使用了。这就导致 BTC 上的交易和 CKB 的交易同构绑定失败。但注意,如果同构绑定失败,但相关的所有资产均被锁定,那么我们不认为出现了安全性问题。因为这种失败源自交易发起人主观攻击协议,那么TA的所有资产被永久锁定不是问题。
但图示的操作中,我们发现 CKB 上的两个输出,RGB++ cell 的 lock 是 btc_utxo#2,它依赖被 revert 的旧的 BTC 交易,因此被永久锁定,没问题。单另一个 ckb cell 则不受影响。这就造成了安全风险。
因此,我们引入一个新的 lock,暂定名为 btc_time_lock 通过提供额外的锁定逻辑来解决这个问题。
BTC Time Lock
btc_time_lock 的核心参数有三个,分别是 lock_hash,after,和 bitcoin_tx。它具体的含意是:“仅当在参数中指定的 bitcoin_tx 被超过 after 个 btc 区块确认后,本 cell 才可以被解锁,且解锁后需要换成 lock_hash 指定的 lockscript(ckb 地址)”。 我们以上面的例子看一下 btc_time_lock 是如何工作的。
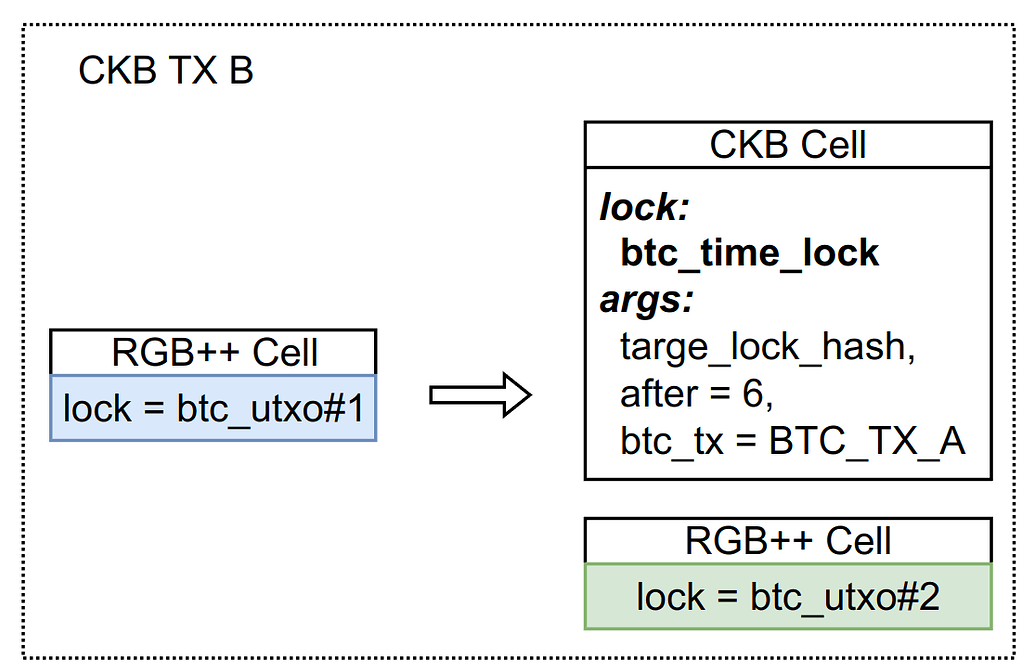
和之前的讨论相同,如果 BTC_TX_A 被 revert 了,对应的 RGB++ Cell 被永久锁定,而其他的 CKB cell 则按照要求被放置自啊 btc_time_lock 中,且他们被解锁的条件是 BTC_TX_A 经过了 6 个区块确认。那么显然由于 BTC_TX_A 不存在而因此被永久锁定。反过来讲,如果 6 个 btc 确认后,BTC_TX_A 仍然存在,那么该 CKB Cell 就可以正常使用。
总结
总结来说,RGB++ 不论在 L1 还是在 L2 上都可以获得与 Bitcoin 相同级别的安全性,在 L1 和 L2 Jump 时,RGB++ 协议额外要求资产锁定 6 个或更多的 BTC 区块,以获得在跨层使用时一致的安全性。RGB++ 协议在不妥协安全性的前提下为 BTC 网络进行了图灵完备的补充和性能的扩展。
致谢
Special thanks to Ren Zhang , Ian , and c4605 for feedback and discussion.
The RGB receiver optimization approach is inspired by Jason Cai .
🔗👉查看原文,获得更多精彩留言。